V roce 1821 Christian Oersted zjistil, že kolem vodiče, kterým prochází elektrický proud, se vytváří magnetické pole.
Tento poznatek vedl Michaela Faradaye k otázce, zda by mohl existovat jev opačný. Tedy, že přítomnost magnetického pole by vyvolala průchod elektrického proudu vodičem. Deset let prováděl Michael Faraday pokusy s cívkou a magnety. Měnil polohu magnetu vzhledem k cívce a ampérmetrem se snažil naměřit elektrický proud. Zjistil, že pokud magnet a cívka jsou navzájem v klidu (magnetické pole se s časem nemění), žádný proud cívkou neprochází. Jestliže ale se magnet vzhledem k cívce pohybuje, ručička ampérmetru se vychýlí.
Magnetické pole, které se s časem mění, se nazývá nestacionární magnetické pole.
Elektromagnetická indukce je děj, při kterém se vlivem vnějšího nestacionárního magnetického pole ve vodiči indukuje napětí a jestliže je vodič součástí uzavřeného obvodu, začne procházet indukovaný elektrický proud.
Příčinou tohoto indukovaného proudu není žádný zdroj elektrického napětí, ale pouze přítomnost nestacionárního magnetického pole v okolí vodiče.
Velikost indukovaného napětí závisí na:
Abychom mohli elektromagnetickou indukci popsat kvantitativně, zavádíme fyzikální veličinu magnetický indukční tok Φ.
Magnetický indukční tok
Skalární fyzikální veličina
Značka: Φ
Jednotka: weber Wb, $ [Φ] = T \cdot m^2 = Wb $
Pro velikost magnetického indukčního toku závitu platí:
$$ Φ = B \cdot S \cdot cos \, \alpha $$
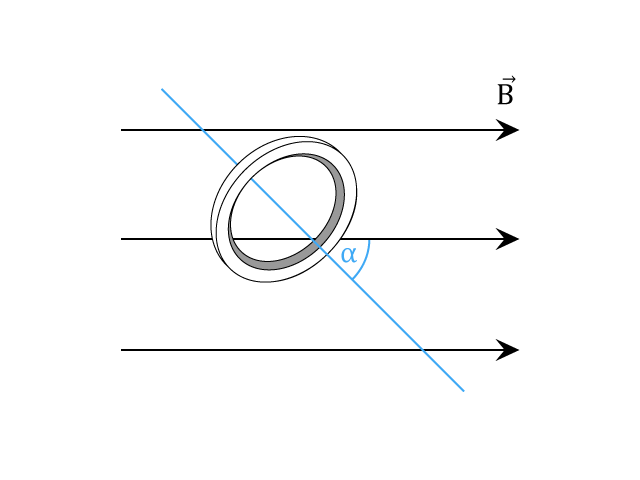
Magnetický indukční tok cívkou s N závity vypočítáme podle vztahu:
$$ Φ = N \cdot B \cdot S \cdot cos \, \alpha $$
Vidíme, že velikost magnetického indukčního toku závisí na:
Největší magnetický indukční tok vzniká, jestliže je závit kolmý k magnetickým indukčním čarám (α = 0°), nulovou hodnotu má, pokud je orientován ve směru magnetických indukčních čar (α= 90°).
a) kolmý ke smyčce
b) svírá se smyčkou úhel 60°
c) rovnoběžný se smyčkou
Po provedení mnoha experimentů s cívkami a magnety se v roce 1831 podařilo Michaelu Faradayovi dokázat, že časově proměnné magnetické pole indukuje ve vodiči napětí Ui. Na základě svých experimentů formuloval zákon elektromagnetické indukce.
Indukované elektromotorické napětí je rovno záporné časové změně magnetického indukčního toku.
$ {U_i} = - \frac{\Delta Φ}{\Delta t} $
Jaké napětí se indukuje ve vodivé smyčce, změní-li se magnetický indukční tok z nulové na $ 1 \, Wb $ za $ 0,5 \, s$?
Znaménko mínus odpovídá Lenzovu zákonu, který si nyní vysvětlíme.
Z animace je zřejmé, že cívka se vždy vychýlí ve směru pohybu magnetu. Jestliže magnet do cívky zasouváme, cívka se od magnetu odpuzuje. Je to proto, že cívka se chová jako magnet orientovaný k tyčovému magnetu stejným pólem. Jestliže magnet vysuneme, cívka se k magnetu přitahuje. Cívka se tedy chová jako magnet orientovaný k tyčovému magnetu opačným pólem.
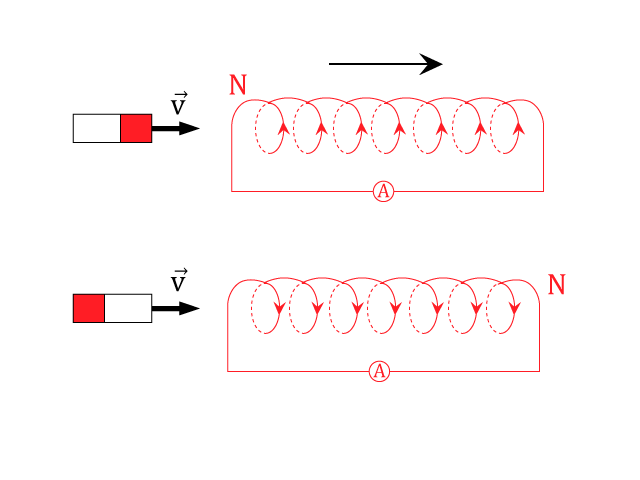

Lenzův zákon
Nyní můžeme formulovat Lenzův zákon:
Indukovaný elektrický proud má takový směr, aby svým magnetickým polem bránil změně, která ho vyvolala.
Zapojíme-li rezistor, cívku a žárovky podle schématu a uzavřeme spínač, začne obvodem procházet elektrický proud. Zatímco žárovka ve větvi s rezistorem začne svítit okamžitě, žárovka ve větvi s cívkou se rozsvítí později.
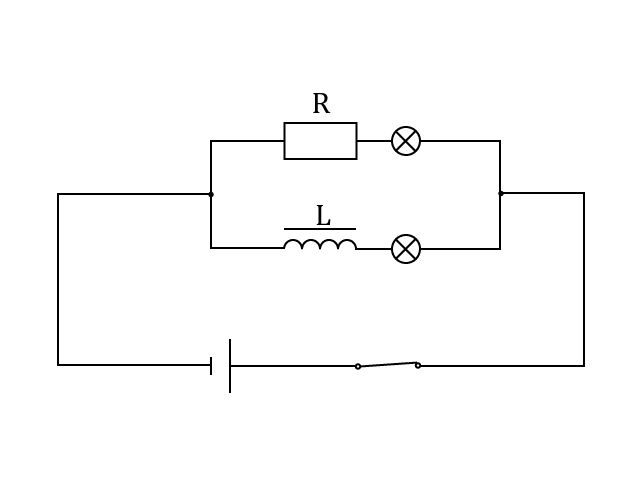
Příčinou je jev, který nazýváme vlastní indukce. Po uzavření obvodu začne cívkou procházet proud vyvolaný zdrojem napětí. V cívce se vytváří nestacionární magnetické pole, a proto současně začne obvodem procházet proud indukovaný, který je opačně orientovaný. Na koncích cívky je tedy indukované napětí, které má opačnou polaritu než je napětí zdroje. Výsledkem je, že po uzavření obvodu s cívkou nedosáhne proud ihned plné velikosti, ale po určitou dobu narůstá a žárovka se rozsvítí později. Jakmile proud dosáhne ustálené hodnoty, přestane se v cívce indukovat napětí a přestane procházet indukovaný proud.
Vlastní indukce je jev, kdy vzniká indukované napětí ve vodiči v důsledku změn vlastního magnetického pole, které vytváří proud ve vodiči.
Tak jako je charakteristikou rezistoru odpor R, tak charakteristikou cívky je indukčnost L.
Indukčnost
Skalární fyzikální veličina
Značka: L
Jednotka: henry H
Výpočet: $ [L] = V \cdot s \cdot A^{-1} = Wb \cdot A^{-1} = H $
Jestliže se za dobu Δt změní elektrický proud o ΔI, změní se magnetický indukční tok cívkou o ΔΦ. V cívce se indukuje napětí:
$ {U_i} = - \frac{\Delta Φ}{\Delta t} = - L \cdot \frac{\Delta I}{\Delta t} $
a) indukčnost cívky
b) počet závitů